Chapitre 7 - Fonctions affines et problèmes du premier degré

Reconnaitre une fonction affine, donnée par son expression.
Donner le sens de variation d’une fonction affine en regardant le signe de $a$ dans son expression
Tracer la représentation graphique d’une fonction affine dont on connait l’expression.
Déterminer l’expression algébrique d’une fonction affine à partir de sa représentation graphique.
Déterminer l’expression algébrique d’une fonction affine connaissant les images de deux valeurs.
Dresser le tableau de signe d’une fonction affine dont on connait l’expression algébrique.
Rechercher, par le calcul, le ou les antécédents d'un nombre par une fonction affine.
Résoudre un problème se ramenant à une équation ou une inéquation du premier degré.
Savoir vérifier graphiquement un résultat trouvé par le calcul
Savoir vérifier par le calcul, un résultat trouvé graphiquement.

IFonctions linéaires et fonctions affines

1Définitions et représentation graphique

Une fonction affine $f$ a une expression de la forme $f (x)=a x+b$ où $a$ et $b$ sont deux nombres réels.
$a$ est appelé le coefficient directeur et $b$ l'ordonnée à l'origine.
Si $b=0$, alors $f (x)=a x$ est l'expression d'une fonction linéaire

Quelques exemples de fonctions affines : $$ \begin{array}{lllll} f (x) &=& 2 x + 3 & & (a = 2 ; b=3)\\ g (x) &=& 6 & & (a = 0 ; b=6)\\ h (x) &=& -x + 0,5 & & (a=-1 ; b=0,5)\\ k (x) &=& \frac{2 x}{3} + 1 & & (a=\frac{2}{2}; b=3)\\ l (x) &=& 1 + 2 x & & (a=2; b=1)\\ \end{array} $$ Les fonctions suivantes ne sont pas des fonctions affines : $$ f (x) = x^2 + 3 $$ $$ g (x) = \frac{2}{x} + 1$$ $$ h (x) = \sqrt{x} + 1 $$

La représentation graphique de toute fonction affine est une droite non-verticale :

Nous raisonnons sur l'exemple $f (x) = -2 x + 1$. Afin de tracer la droite représentative $D_f$ :

On choisit deux abscisses $x_1$ et $x_2$. Par exemple $x_1 = 0$ et $x_2 = 2$
On calcule $f (x_1)$ et $f (x_2)$. Ici, $f (x_1) = -2\times 0 + 1 = 1$ et $f (x_2)=-2 \times 2 + 1 = -3$
On place les points $M_1 (x_1; f (x_1))$ et $M_2 (x_2;f (x_2))$. Ici, $M_1 (0;1)$ et $M_2 (2;-3)$
On relie les deux points pour obtenir la droite représentative

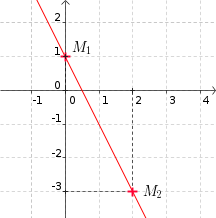
Cette méthode simple ne fonctionne que parce que la courbe représentative est une droite. Elle est à exclure pour une fonction pas affine
Peu importent les valeurs de $x_1$ et $x_2$, attention toutefois à prendre des valeurs suffisament écartées et qui rentrent sur le graphique

2Ordonnée à l'origine et coefficient directeur

On donne plusieurs manières de trouver $a$ et $b$ à partir d'une représentation graphique, ou à partir de valeurs données. Il est parfois possible de raisonner par le calcul, ou par lecture graphique :

APar le calcul

Calcul du coefficient directeur :

Soit une droite $D$ représentant une fonction affine d'équation $f (x) = a x + b$ :

alors, pour tous points $M_1 (x_1;y_1)$ et $M_2 (x_2;y_2)$ distincs, on a : $$a = \frac{y_2 - y_1}{x_2 - x_1}$$

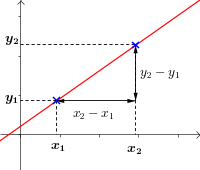
Le résultat est le même quelques soient les points choisis

Calcul de l'ordonnée à l'origine :

Si on connaît le coefficient directeur $a$ (mais pas $b$), et un point $M (x_M, y_M)$ de la droite représentative, il est possible de calculer $b$. On raisonne sur l'exemple suivant :

Le coefficient directeur $a$ vaut $2$ et la droite passe par le point $M (3;2)$.
L'équation est donc $f (x) = 2 x + b$. On sait que $M$ est sur la droite, donc $f (3) = 2$.
On utilise l'équation pour $x=3$: $2 \times 3 + b = 2$, donc $6 + b = 2$, donc $b=2-6 = -4$ Finalement, on a l'équation complète $f (x) = 2 x - 4$

En général, $b = y_M - a x_M$

On utilise ses deux techniques pour trouver l'équation d'une droite à partir de deux de ses points :

Soit $D$ une droite passant par les points $M (3;4)$ et $N (1;0)$.

$a = \frac{y_M - y_N}{x_M - x_N} = \frac{4 - 0}{ 3 - 1} = \frac{4}{2} = 2$
$b = y_M - a x_M = 4 - 2\times 3 = -2$ (même résultat avec $N$)

Donc $D$ admet pour équation $f (x) = 2 x - 2$

BPar lecture graphique

Lecture de l'ordonnée à l'origine $b$ :

$b$ peut se lire la où la droite coupe l'axe de ordonnées.

Lecture de l'ordonnée à l'origine $a$ :

En partant d'un point quelconque de la droite, on avance horizontalement de une unité, il faut alors $a$ unités verticales pour rejoindre la droite (positif vers le haut, négatif vers le bas)

la droite monte de $a=1$ quand on avance de 1 carreau
la droite coupe les ordonnées à $b=2$
Donc l'équation est $f (x) = x - 2$

la droite descend de $a=-2$ quand on avance de 1 carreau
la droite coupe les ordonnées à $b=1$
Donc l'équation est $f (x) = 2 x - 2$

3Sens de variations

On considère une fonction affine d'expression $f (x)=a x + b$, alors sa droite représentative est :

croissante si $a \gt 0$
décroissante si $a \lt 0$
constante $a=0$

Les tableaux de variations sont donc les suivants :

Pour $a \gt 0$ :	Pour $a \lt 0$ :
$$ \begin{array}{c\|lcr\|} x &-\infty & & & & +\infty\\\hline f (x) & & & \nearrow & & \\ \end{array} $$	$$ \begin{array}{c\|lcr\|} x &-\infty & & & & +\infty\\\hline f (x) & & & \searrow & & \\ \end{array} $$

IIInéquations et études de signes

Pour \(a \gt 0\) :	Pour \(a \lt 0\) :
$$ \begin{array}{c\|lcr\|} x &-\infty & & & & +\infty\\\hline f (x) & & & \nearrow & & \\ \end{array} $$	$$ \begin{array}{c\|lcr\|} x &-\infty & & & & +\infty\\\hline f (x) & & & \searrow & & \\ \end{array} $$